Multiplying algebraic fractions worksheet
N2f — Applying the four operations to fractions — this is fundamental, multiplying algebraic fractions worksheet. A4a — Simplifying and manipulating algebraic expressions A4b — Multiplying a single term over a bracket Multiplying algebraic fractions worksheet — Factorising basic A4d — Soft play bridgeton two or more brackets A4e — Factorising quadratics A4i — Index laws. Teacher resources for Part 1. Teachers : log in to access the following: Slides in PPTX with click-to-reveal answers Slides in PDF one slide per page, suitable for importing into IWB software Worksheet with space for student work Handout slides with exercises only; 4 per page for reduced printing Worked solutions to all questions Mashup activity: Subprime.
By using this website, you agree to our use of cookies. We use cookies to provide necessary site functionality and provide you with a great experience. Your form has been submitted. Please check your email for a copy of your responses. If you're accepted, you'll receive an email with a link to checkout.
Multiplying algebraic fractions worksheet
Here we will learn about multiplying and dividing algebraic fractions, including algebraic fractions with monomial and binomial numerators and denominators. Multiplying and dividing algebraic fractions is the skill of multiplying and dividing two or more fractions that contain algebraic terms. To do this we must combine our knowledge of multiplying and dividing fractions with our understanding of algebra. Step-by-step guide: Multiplying and dividing fractions. Step-by-step guide: Algebraic terms. To multiply with fractions, we multiply the numerators together, and multiply the denominators together. This is the same for algebraic fractions, but we need to take extra care when multiplying algebraic terms or expressions. To divide with fractions, we first write the reciprocal of the dividing fraction and then multiply the numerators together, and multiply the denominators together. Includes reasoning and applied questions. Multiply the numerators together and multiply the denominators together. Note that you can leave algebraic products in factorised form. However, to help with step 2 it is best to check that they are fully factorised. The terms in the bracket here do not share a common factor other than 1, and therefore the expression is fully factorised. Simplify the fraction if possible.
The bracket of the numerator is the difference of two squares and can be factorised into double brackets. You also have the option to opt-out of these cookies.
Here we will learn about algebraic fractions , including operations with fractions, and solving linear and quadratic equations written in the form of algebraic fractions. The main aim of this lesson is to understand how to solve equations that include algebraic fractions. All the examples above are expressions whereas the examples below are equations as we can find specific values for x for each example to solve the equation. It is important to be able to simplify algebraic fractions into their simplest form. If you need to practice this or need a quick refresher, see the lesson on simplifying algebraic fractions for further information. Step-by-step guide: Simplifying algebraic fractions. Here, the denominator of the fraction contains the variable, so we first need to get the variable out of the denominator.
Multiplying fractions: When a fraction is multiplied by another fraction the resultant is a fraction or a whole number. We know, a fraction has two parts: numerator and denominator. Thus, when we multiply any two fractions, then numerators and denominators are multiplied, respectively. Multiplying fractions is not like the addition or subtraction of fractions, where the denominators of both the fractions should be the same. Two fractions can be multiplied easily, even if the denominators are different.
Multiplying algebraic fractions worksheet
Log In Join. View Wish List View Cart. Middle school. High school. Adult education. Resource type. Independent work. Independent work packet. Graphic organizers.
Video game store london
This topic is relevant for:. Your form has been submitted. These cookies will be stored in your browser only with your consent. Simplifying fractions incorrectly 2 Seeing the same term on the numerator and denominator allow the misconception that they can both be cancelled. Multiplying algebraic fractions examples. Necessary cookies are absolutely essential for the website to function properly. Theory Dividing Algebraic Fractions. Simplify the fraction if possible. Factoring Polynomials. Make it :.
Teachers and students alike might argue this concept is more daunting than leaping from subtraction and addition to multiplication.
We use essential and non-essential cookies to improve the experience on our website. The resultant answer will be. Seeing the same term on the numerator and denominator allow the misconception that they can both be cancelled. Still stuck? In order to access this I need to be confident with: Fractions Simplifying fractions Adding and subtracting fractions Rearranging equations Solving equations Quadratic equations factorisation Quadratic formula Expanding brackets Simultaneous equations. For example, Incorrectly choosing to cross multiply, The correct solution is Common denominators are not needed When we add or subtract fractions we must ensure there is a common denominator. Teachers : log in to access the following: Slides in PPTX with click-to-reveal answers Slides in PDF one slide per page, suitable for importing into IWB software Worksheet with space for student work Handout slides with exercises only; 4 per page for reduced printing Worked solutions to all questions Mashup activity: Subprime. Worksheets E-books Bundles Contact Login. When we are multiplying fractions, we can choose to write the fractions with a common denominator but this simply makes the process lengthier and it is not necessary. I am passionate about travelling and currently live and work in Paris. Polynomial Worksheet. The parentheses in the numerator will be opened and the signs of all the terms inside it will be reversed:. The bracket of the numerator is the difference of two squares and can be factorised into double brackets. N2f — Applying the four operations to fractions — this is fundamental.

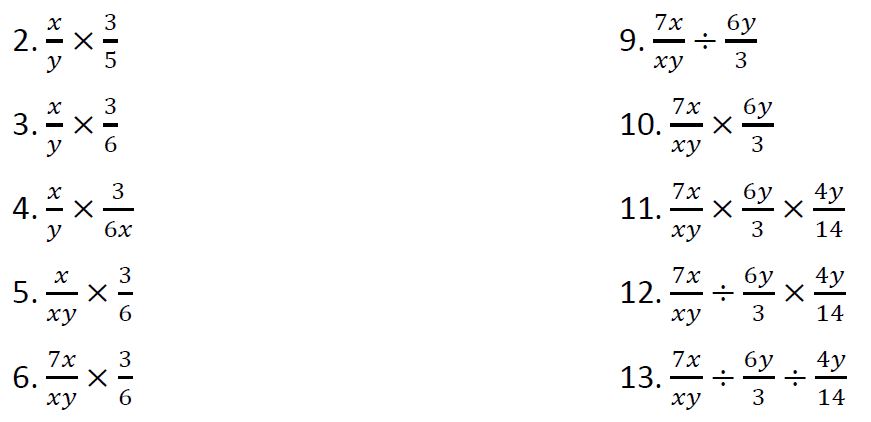
Let's return to a theme