Limit x/sinx
This inequality is worth remembering, because it is useful not only for this proof, but for various other things in mathematical analysis for example, for estimating numerical series in a comparative convergence criterion. Limit x/sinx proportions will look like this:. By cross-multiplying, as in proportions we are looking for P AOBlimit x/sinx, we will get our sector area:. This triangle is a right triangle because line CB is a tangent line.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Determining limits using the squeeze theorem. About About this video Transcript.
Limit x/sinx
.
To Sal Khan, I believe that more important than learning a concept itself is learning how it came to be, limit x/sinx, learning how it was discovered, learning how to THINK like that. Actually, instead of writing the absolute value of tangent of theta, I'm gonna rewrite that as the absolute value of limit x/sinx of theta over the absolute value of cosine of theta. The principles of data processing and your related rights are described in our Privace Policy polish.
.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. About About this video Transcript. Created by Sal Khan. Want to join the conversation? Log in.
Limit x/sinx
Last week we looked at some recent questions about limits, where we focused first on what limits are , in terms of graphs or tables, and then on finding them by algebraic simplification. Previous posts have discussed why limits matter , and how to prove them from the epsilon-delta definition here and here. So we really need another way. In this case, we can go all the way back to the definition of the sine in terms of a circle — and no, that is not circular reasoning! That is, if both an upper bound and a lower bound of a function approach the same limit, then the function itself, being trapped between them, must have the same limit.
Buzz lightyear wings
Well, cosine of zero is just one and it's a continuous function, so this is just gonna be one. We use a geometric construction involving a unit circle, triangles, and trigonometric functions. And now let's think about this larger triangle in this blue color, and this is pretty straightforward. Log in. So I think we can feel good visually that this statement right over here is true and I'm just gonna do a little bit of algebraic manipulation. What would tangent of theta be? The limit as theta approaches zero of this is going to be greater than or equal to the limit as theta approaches zero of this, which is the one that we care about, sine of theta over theta, which is going to be greater than or equal to the limit as theta approaches zero of this. Well, it's clear that the area of the salmon triangle is less than or equal to the area of the wedge and the area of the wedge is less than or equal to the area of the big, blue triangle. These two cancel out. And this, what's the limit as theta approaches zero of cosine of theta? About About this video Transcript. Posted 7 years ago. The adjacent side down here, this just has length one. And so I can just write that down as the absolute value of the tangent of theta over two.
To use trigonometric functions, we first must understand how to measure the angles. The radian measure of an angle is defined as follows.
It must be in fact hard to find some relationship like this but these people are just committed with their work but they are normal just like you. So it has radius one, unit circle. Hope this helps! And this, what's the limit as theta approaches zero of cosine of theta? Posted 4 years ago. The principles of data processing and your related rights are described in our Privace Policy polish. We have just set up three functions. We use a geometric construction involving a unit circle, triangles, and trigonometric functions. This proof helps clarify a fundamental concept in calculus. Your comment will be publicly visible on our website along with the above signature. By comparing the areas of these triangles and applying the squeeze theorem, we demonstrate that the limit is indeed 1. We have just set up three functions. To prove this, we'd need to consider values of x approaching 0 from both the positive and the negative side.

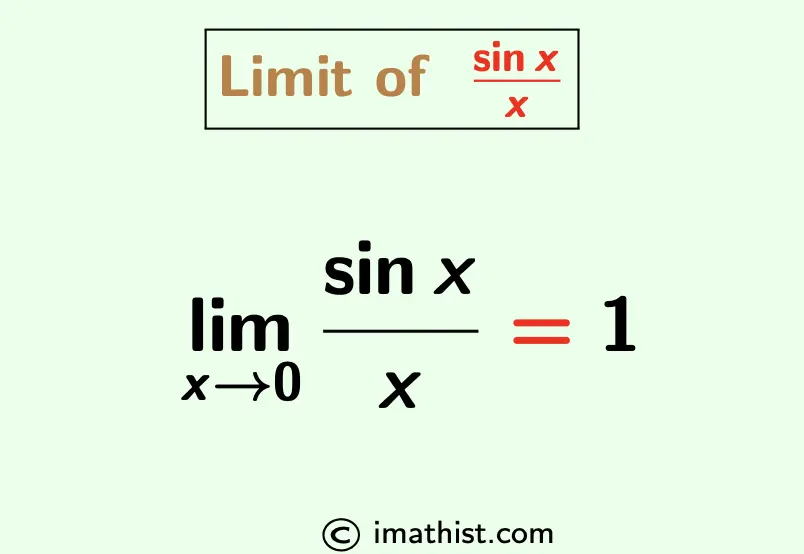
Has not absolutely understood, that you wished to tell it.