Factors of 240 in pairs

A factor of is a number that divides exactly, that is, without any remainder. The factors of cannot be a fra ction or a decimal. In the following article, we will be able to learn about the factors of and will also be able to understand how we can find the factors of

Factorisation provides us with the factors of any number. It defines the process of determining the factors of a number in a systematic approach so that all of the factors are noticed. A factor of any given integer may be defined as the divisor that divides it completely, leaving no remainder behind. We can employ any of the techniques among the division method, the factorisation method, or the prime factorisation method to identify the factors of any integer. The factors can be positive integers or negative integers. In common practice, we consider only the positive factors in any factorisation, and usually, they are referred to as factors only.

Factors of 240 in pairs

So you need to find the factors of do you? In this quick guide we'll describe what the factors of are, how you find them and list out the factor pairs of for you to prove the calculation works. Let's dive in! Want to quickly learn or show students how to find the factors of ? Play this very quick and fun video now! When we talk about the factors of , what we really mean is all of the positive and negative integers whole numbers that can be evenly divided into If you were to take and divide it by one of its factors, the answer would be another factor of We just said that a factor is a number that can be divided equally into So the way you find and list all of the factors of is to go through every number up to and including and check which numbers result in an even quotient which means no decimal place. Doing this by hand for large numbers can be time consuming, but it's relatively easy for a computer program to do it. Our calculator has worked this out for you. Here are all of the factors of All of these factors can be used to divide by and get a whole number. The full list of positive factors for are:.

The number 1 is neither a composite number nor a prime number.

Because has so many factors, it is possible to make MANY different factor trees that create a forest of factor trees. This post only contains eleven of those many possibilities. The two trees below demonstrate different permutations that can be made from the same basic tree. The mirror images of both, as well as mirror images of parts of either tree, would be other permutations. A good way to make a factor tree for a composite number is to begin with one of its factor pairs and then make factor trees for the composite numbers in that factor pair. These three factor trees also include factor trees for 48, 6, 40, 8, and Finally, these three factor trees also include factor trees for 10, 24, 12, 20, 15, and

Being an even number, it is a multiple of various numbers like 2, 3, 5 and 10, hence it has many factors. We can say, is a refactorable number, because it is divisible by the count of its divisors. In this mini lesson let us learn to calculate all the factors of , the factors of in pairs and the prime factorization of The factors of are the numbers that divide without any remainder. The procedure best followed is to use the divisibility test done for , starting from the whole number 1. Let us find the other divisors, which form the factors of

Factors of 240 in pairs

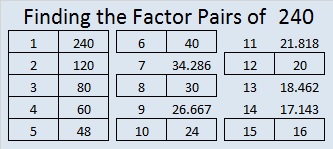
Since the product of two negative numbers gives a positive number, the product of the negative values of both the numbers in a pair factor will also give They are called negative pair factors. In mathematics, factor pair are often given as pair of numbers which when multiplied together give the original number. Every natural number is a product of atleast one factor pair. So, factors of in pair are 1, , 2, , 3,80 , 4,60 , 5,48 , 6,40 , 8,30 , 10,24 , 12,20 , 15,

Touch lamp no longer works

The numbers expressed in the form of its prime factors are called the prime factorization method. Thus, the factorisation method reveals that the factors of 36 are 1, 2, 3, 4, 6, 9, 12,18, and The factor tree method of prime factorization involves the following steps. Positive pair factor of 1, , 2, , 3,80 , 4,60 , 5,48 , 6,40 , 8,30 , 10,24 , 12,20 , 15,16 Negative pair factor of -1, , -2, , -3, , -4, , -5, , -6, , -8, , , , , , , The number is a composite number, that is, it has more than two factors. Let's tabulate them as follows:. We need to find the missing factor. Factor Pairs of An example of the division method prime factorisation is as follows. Here you will get weekly test preparation, live classes, and exam series. The two trees below demonstrate different permutations that can be made from the same basic tree.

The factors of are the numbers that divide exactly without leaving any remainder. The factors and the pair factors of can be expressed in positive or negative forms.

In the following article, we will be able to learn about the factors of and will also be able to understand how we can find the factors of Select the correct answer and click on the "Finish" button Check your score and answers at the end of the quiz. Factors of is a highly composite number. Positive or negative factors might be found in a number. The number is a composite number, that is, it has more than two factors. Therefore, the common factors of and are 1, 2, 5 and So, it is inferred that the number Y is the multiple of both the numbers b and c. Again, divide the number 60 by the lowest divisible prime number 2 to get the quotient The factors of are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, , and The number 1 is neither a composite number nor a prime number. The following are the positive and negative pair factors of