Cos 2 2x sin 2 2x
Please ensure that your password is at least 8 characters and contains each of the following:. Enter a problem Trigonometry Examples Popular Problems.
We recall the Pythagorean trig identity and rearrange it for cos squared x to make [1]. We recall the double angle trig identity and rearrange it for sin squared x to make [2]. We then substitute [2] into [1] and simplify to make identity [3]. As you can see identity 3 is almost like the cos squared part of our integration problem except it has 2x for the angle. If we multiply the angles on both sides by 2, then as you can see, we get the cos squared 2x term, as shown above.
Cos 2 2x sin 2 2x
.
List the new angles.
.
Cos2x is one of the important trigonometric identities used in trigonometry to find the value of the cosine trigonometric function for double angles. It is also called a double angle identity of the cosine function. The identity of cos2x helps in representing the cosine of a compound angle 2x in terms of sine and cosine trigonometric functions, in terms of cosine function only, in terms of sine function only, and in terms of tangent function only. Cos2x identity can be derived using different trigonometric identities. Let us understand the cos2x formula in terms of different trigonometric functions and its derivation in detail in the following sections.
Cos 2 2x sin 2 2x
In mathematics, an "identity" is an equation which is always true, regardless of the specific value of a given variable. Need a custom math course? K12 College Test Prep. Logically, mathematical identities are tautologies; that is, they are expressions which restate the same expression in a different way. In other words, the identities allow you to restate a trig expression in a different format, but one which has the exact same value. There are loads of trigonometric identities, but the following are the ones you're most likely to see and use. Notice how a "co- something " trig ratio is always the reciprocal of some "non-co" ratio.
Mafia consigliere
Separate fractions. Take the inverse tangent of both sides of the equation to extract from inside the tangent. And we get a simpler expression, however it still has a cos squared term that makes integration prohibitive. Simplify the numerator. We recall the Pythagorean trig identity and rearrange it for cos squared x to make [1]. We repeat the steps using the Pythagorean trig identity and the double angle identity, except we get the sin squared x term as shown at [4]. Integration Solutions Donate. Convert from to. Move to the left of. We integrate the second term and get the answer as shown above in red.
Please ensure that your password is at least 8 characters and contains each of the following:. Enter a problem
Take the inverse tangent of both sides of the equation to extract from inside the tangent. Add to to find the positive angle. The distance between and is. Separate fractions. As you can see, we now have an equivalent trig identity that we could integrate, however it still requires simplification. The period of the function is so values will repeat every radians in both directions. Convert from to. Add to every negative angle to get positive angles. Find the period of. The tangent function is negative in the second and fourth quadrants. We integrate the second term and get the answer as shown above in red. Hence, our original integration problem can be writtin in a new form as shown above. Consolidate the answers. If we multiply the angles on both sides by 2, then as you can see, we get the cos squared 2x term, as shown above.

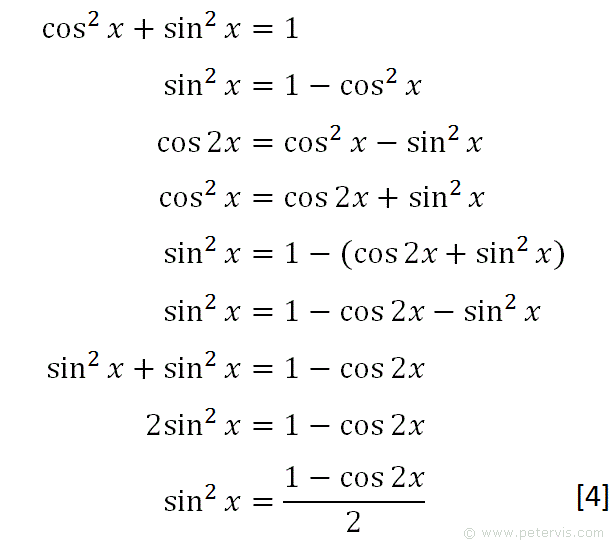
Just that is necessary, I will participate. Together we can come to a right answer. I am assured.
I understand this question. Is ready to help.