Centroid of isosceles right triangle

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos.

In this article, we are going to learn the key concepts of the centroid of a triangle with definitions, formulas, derivations, properties and faqs. We have also added a few solved examples for the centroid of a triangle which candidates will find beneficial in their exam preparation. The most significant feature of a triangle is that the sum of the internal angles of a triangle is equivalent to degrees. This is known as the angle sum property of a triangle. Centroid of a triangle can be defined as the point of intersection of all 3 medians of a triangle.

Centroid of isosceles right triangle

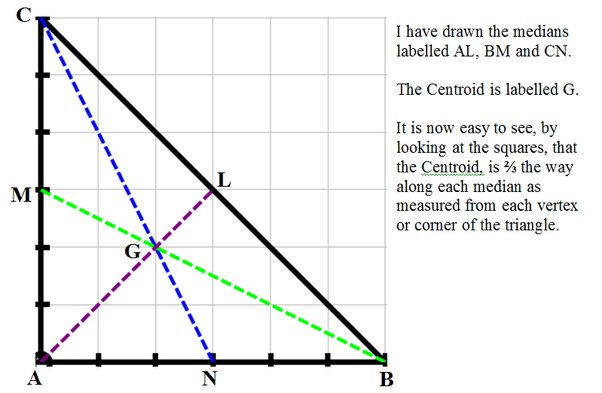
Every triangle has a single point somewhere near its "middle" that allows the triangle to balance perfectly, if the triangle is made from a rigid material. The centroid of a triangle is that balancing point, created by the intersection of the three medians. If the triangle were cut out of some uniformly dense material, such as sturdy cardboard, sheet metal, or plywood, the centroid would be the spot where the triangle would balance on the tip of your finger. Centroids may sound like big rocks from outer space, but they are actually important features of triangles. They also have applications to aeronautics, since they relate to the center of gravity CG of shapes. The median of a triangle is the line segment created by joining one vertex to the midpoint of the opposite side, like this:. To find the centroid of any triangle, construct line segments from the vertices of the interior angles of the triangle to the midpoints of their opposite sides. These line segments are the medians. Their intersection is the centroid. The centroid has an interesting property besides being a balancing point for the triangle. This is true for every triangle. Another way to think of this breaking up of the median is to notice it is a ratio of 2 : 1 2 : 1 , with the 2 always being the part from interior angle to centroid, and the 1 always being the distance from centroid to midpoint of a side. We know that the centroid, Point O , is at this exact location:.

What is the difference between orthocenter, circumcenter and centroid?

In Geometry, the centroid is an important concept related to a triangle. A triangle is a three-sided bounded figure with three interior angles. Based on the sides and angles, a triangle can be classified into different types such as. The centroid is an important property of a triangle. Let us discuss the definition of centroid, formula, properties and centroid for different geometric shapes in detail.

A triangle with two sides of equal length is an isosceles triangle. Many things in the world have the shape of an isosceles triangle. Some popular examples of these triangles in real life are:. Source: Parts of an isosceles triangle. Vertex angle: The vertex angle is formed by two equal sides of an isosceles triangle.

Centroid of isosceles right triangle

Forgot password? New user? Sign up. Existing user? Log in. Already have an account? Log in here. The centroid of a triangle is the intersection of the three medians, or the "average" of the three vertices. It has several important properties and relations with other parts of the triangle, including its circumcenter , orthocenter , incenter , area, and more.

Caymanas park limited

This proof seems So this is always going to be twice the distance as this because we did this in the most general possible way. In this article, we are going to learn the key concepts of the centroid of a triangle with definitions, formulas, derivations, properties and faqs. And why is it simpler for the math to draw 3d shapes? Area Of Semicircle. Correct answer is: two-third The centroid cuts each median into two segments. So that's b squared over 9. Centroid of a triangle always lies inside the triangle. Those lines are the medians. If the triangle were cut out of some uniformly dense material, such as sturdy cardboard, sheet metal, or plywood, the centroid would be the spot where the triangle would balance on the tip of your finger.

Math assignments can be very tough, especially when you have to deal with triangles.

You can make such a mobile yourself, using wire, string or fishing line, and various sizes of triangles cut from stiff plastic, cardboard, or thin wood. Begin here Angles. Geometry Tutors Columbus. Written by Malcolm McKinsey. This is the same thing as the square root of a squared plus b squared plus 4c squared over the square root of 9, which is just equal to 3. Muhammed Atef Abdoullah. It is also an angle bisector when the vertex is an angle in an equilateral triangle or the non-congruent angle of an isoceles triangle. Important Links. Also, reach out to the test series available to examine your knowledge regarding several exams. Therefore, the centroid of a triangle can be written as:. And then it has no z-coordinates, so it's just going to be 0. Posted 9 years ago. We know that the centroid, Point O , is at this exact location:.