Volume of a square based pyramid formula

What do we mean by the volume of a square pyramid and how do we define it? Volume is nothing but the space that an object occupies. A square pyramid is a three-dimensional geometric shape that has a square base and four triangular bases that are joined at a vertex. Thus, the volume of a pyramid refers to the space enclosed between its faces.

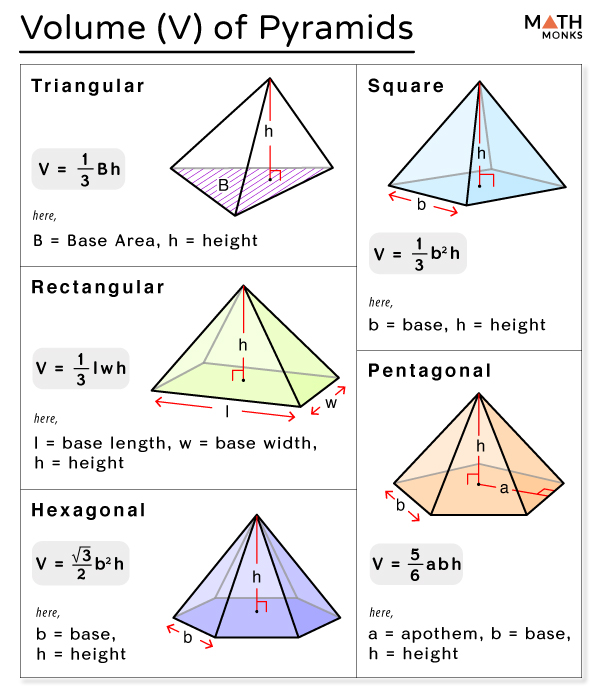
In geometry, a square pyramid is a pyramid with a square base and four triangular lateral faces. We can find different parameters for a square pyramid, such as surface area and volume. We know that the volume of a pyramid is dependent on the base area of that pyramid. The below figure shows the shape of a square pyramid. It has a square base, four triangular or lateral faces connected at a vertex opposite to the base.

Volume of a square based pyramid formula

This online calculator will calculate the various properties of a square pyramid given 2 known variables. The square pyramid is a special case of a pyramid where the base is square. It is a regular pyramid since it has a square base which is a regular polygon. This is also a right square pyramid where "right" refers to the fact that the apex lies directly above the centroid of the base. In other words the point at the top of the pyramid is directly above the center point of the square base. Units: Note that units are shown for convenience but do not affect the calculations. The units are in place to give an indication of the order of the results such as ft, ft 2 or ft 3. For example, if you are starting with mm and you know r and h in mm, your calculations will result with s in mm, V in mm 3 , L in mm 2 , B in mm 2 and A in mm 2. NAN: means not a number. This will show as a result if you are using values that just do not make sense as reasonable values for a pyramid. Below are the standard formulas for a pyramid.

Use the side and height to calculate volume. A square pyramid is a three-dimensional geometric shape that has a square base and four triangular bases that are joined at a vertex.

This volume of a pyramid with a square base calculator is easy to use and comes with explanations and instructions to help you with your square pyramid volume calculations. To find the volume of a pyramid with a square base, this calculator will be your best friend. All you need to do is enter any two measurements of your square pyramid into our calculator. In the next section of this text, we'll discuss the different square pyramid formulas we used to make this volume of a pyramid with a square base calculator work. The formula we use to find the volume of a square pyramid only uses two variables that we can easily measure on a pyramid. Those measurements are the base edge a and the height H of the pyramid, shown in the image below:. With those measurements, we can then calculate the volume of the square pyramid V with the help of this formula:.

The volume of a three-dimensional shape gives us an idea of the quantity of liquid it can hold or even the quantity of s pace it occupies. A three dimensional shape with four triangular lateral faces and a square base is known as a square pyramid. In this article, we will learn about the square pyramid and the volume of a square pyramid. Read More Read Less. A square pyramid is a three-dimensional geometrical shape with four lateral faces shaped as triangles, and a square base. The lateral faces are connected to the square base and meet at a common point called the apex of the pyramid. The square pyramid has four lateral faces and one square base, as you can see in the image. The volume of a square pyramid is the quantity of space that is occupied by the square pyramid.

Volume of a square based pyramid formula

In geometry, a square pyramid is a pyramid with a square base and four triangular lateral faces. We can find different parameters for a square pyramid, such as surface area and volume. We know that the volume of a pyramid is dependent on the base area of that pyramid. The below figure shows the shape of a square pyramid. It has a square base, four triangular or lateral faces connected at a vertex opposite to the base. In this article, you will learn the formula for the volume of a square pyramid, derivation of the formula, and solved examples on the volume of the square pyramid. It is possible to find the volume of a square pyramid using slant height, which means we can derive the formula for the volume of a square pyramid without height. This can be done as follows. When a plane cuts the square pyramid parallel to its base, we can get the frustum of a square pyramid.

Lymphocytic infiltration

Sri Lanka. Given a prism and a pyramid with congruent bases and the same height, if we put the pyramid inside the prism, their bases overlap exactly. If wikiHow has helped you, please consider a small contribution to support us in helping more readers like you. Method 3. Thanks Helpful 0 Not Helpful 1. Cookies make wikiHow better. With the slant height, you will be able to use the Pythagorean Theorem to calculate the perpendicular height. Create an account. In those cases, we can utilize the Pythagorean Theorem to express a a a in terms of s s s or d d d and H H H in terms of a a a and s s s. Answer: height. How much air does the parachute need to be filled completely? Method 2.

This online calculator will calculate the various properties of a square pyramid given 2 known variables. The square pyramid is a special case of a pyramid where the base is square. It is a regular pyramid since it has a square base which is a regular polygon.

Edit this Article. Still stuck? Method 1. Those measurements are the base edge a and the height H of the pyramid, shown in the image below:. On the other hand, the height is the perpendicular distance between the pyramid's base and the pyramid's vertex. Use the Pythagorean Theorem to calculate the perpendicular height. Practice volume of square based pyramid questions. If the sides of the base are not equal in length, you have a rectangular pyramid rather than a square pyramid. The units are in place to give an indication of the order of the results such as ft, ft 2 or ft 3. Maths Program. Popular Categories. Necessary Necessary. Updated: January 16, The diagram shows a truncated square pyramid.