Unit 8 progress check mcq part a ap calc ab

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Unit 1. Unit 2. Unit 3.

Unit 8 progress check mcq part a ap calc ab

.

Search for courses, skills, and videos.

.

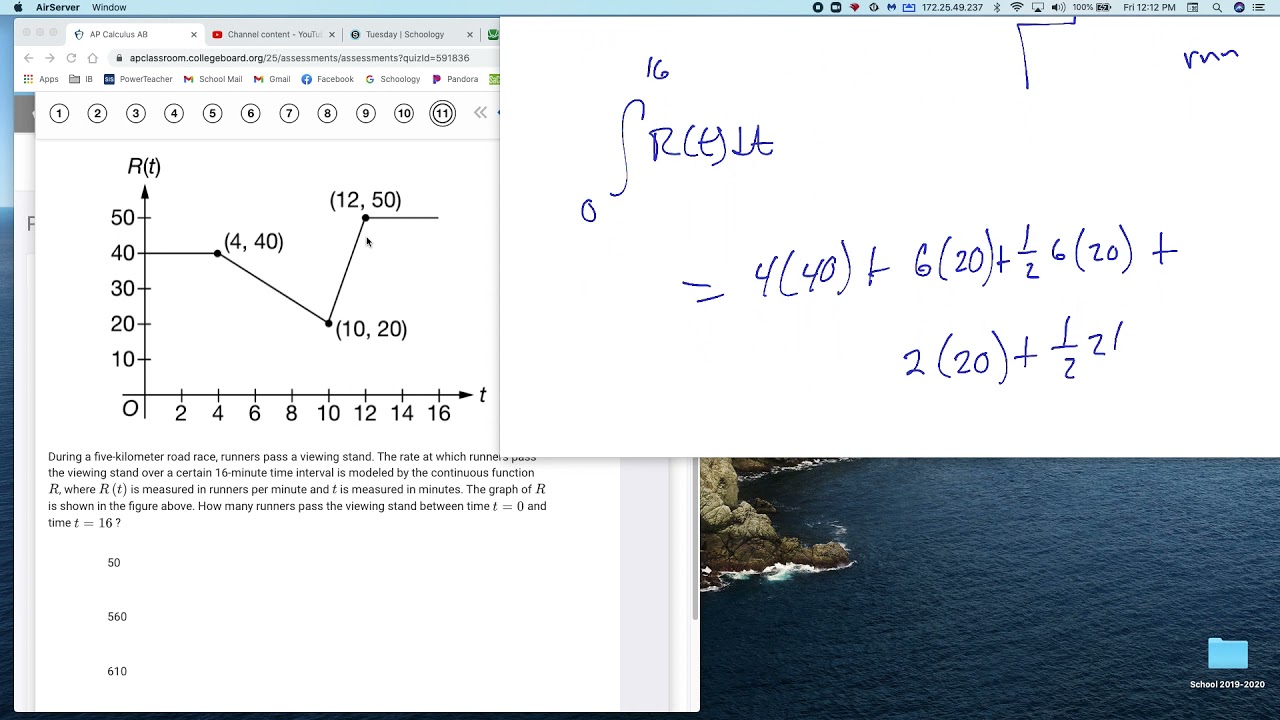
Show all of your work, even though the question may not explicitly remind you to do so. Clearly label any functions, graphs, tables, or other objects that you use. Justifications require that you give mathematical reasons, and that you verify the needed conditions under which relevant theorems, properties, definitions, or tests are applied. Your work will be scored on the correctness and completeness of your methods as well as your s. Answers without supporting work will usually not receive credit.

Unit 8 progress check mcq part a ap calc ab

All Subjects. Exam Skills. Not my favorite color-by-letter. Image Courtesy of Alberto G. For many students in AP Calculus, the multiple-choice section is easier than the free-response section. You'll be asked more straightforward skills-based questions, problems typically don't build off of each other, and you have the power to guess. Still, doing well on the multiple-choice requires good test-taking strategies and lots of practice.

Azir ahai

To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Unit 9. Unit 2: Differentiation: definition and basic derivative rules. Volumes with cross sections: triangles and semicircles : Applications of integration Volume with disc method: revolving around x- or y-axis : Applications of integration Volume with disc method: revolving around other axes : Applications of integration Volume with washer method: revolving around x- or y-axis : Applications of integration Volume with washer method: revolving around other axes : Applications of integration The arc length of a smooth, planar curve and distance traveled : Applications of integration Calculator-active practice : Applications of integration. Modeling situations with differential equations : Differential equations Verifying solutions for differential equations : Differential equations Sketching slope fields : Differential equations. Unit 5: Applying derivatives to analyze functions. Unit 6. Finding the average value of a function on an interval : Applications of integration Connecting position, velocity, and acceleration functions using integrals : Applications of integration Using accumulation functions and definite integrals in applied contexts : Applications of integration Finding the area between curves expressed as functions of x : Applications of integration Finding the area between curves expressed as functions of y : Applications of integration Finding the area between curves that intersect at more than two points : Applications of integration. Unit 1: Limits and continuity. Unit 7: Differential equations. Selecting procedures for calculating derivatives: strategy : Differentiation: composite, implicit, and inverse functions Selecting procedures for calculating derivatives: multiple rules : Differentiation: composite, implicit, and inverse functions Calculating higher-order derivatives : Differentiation: composite, implicit, and inverse functions Further practice connecting derivatives and limits : Differentiation: composite, implicit, and inverse functions Optional videos : Differentiation: composite, implicit, and inverse functions. Course challenge. Unit 3: Differentiation: composite, implicit, and inverse functions.

.

Solving motion problems using parametric and vector-valued functions : Parametric equations, polar coordinates, and vector-valued functions Defining polar coordinates and differentiating in polar form : Parametric equations, polar coordinates, and vector-valued functions Finding the area of a polar region or the area bounded by a single polar curve : Parametric equations, polar coordinates, and vector-valued functions Finding the area of the region bounded by two polar curves : Parametric equations, polar coordinates, and vector-valued functions Calculator-active practice : Parametric equations, polar coordinates, and vector-valued functions. Using the mean value theorem : Applying derivatives to analyze functions Extreme value theorem, global versus local extrema, and critical points : Applying derivatives to analyze functions Determining intervals on which a function is increasing or decreasing : Applying derivatives to analyze functions Using the first derivative test to find relative local extrema : Applying derivatives to analyze functions Using the candidates test to find absolute global extrema : Applying derivatives to analyze functions Determining concavity of intervals and finding points of inflection: graphical : Applying derivatives to analyze functions. Interpreting the meaning of the derivative in context : Contextual applications of differentiation Straight-line motion: connecting position, velocity, and acceleration : Contextual applications of differentiation Rates of change in other applied contexts non-motion problems : Contextual applications of differentiation Introduction to related rates : Contextual applications of differentiation. If you're seeing this message, it means we're having trouble loading external resources on our website. Unit 1: Limits and continuity. Unit 9. Community questions. Defining average and instantaneous rates of change at a point : Differentiation: definition and basic derivative rules Defining the derivative of a function and using derivative notation : Differentiation: definition and basic derivative rules Estimating derivatives of a function at a point : Differentiation: definition and basic derivative rules Connecting differentiability and continuity: determining when derivatives do and do not exist : Differentiation: definition and basic derivative rules Applying the power rule : Differentiation: definition and basic derivative rules Derivative rules: constant, sum, difference, and constant multiple: introduction : Differentiation: definition and basic derivative rules. Unit 6: Integration and accumulation of change. Volumes with cross sections: squares and rectangles : Applications of integration Volumes with cross sections: triangles and semicircles : Applications of integration Volume with disc method: revolving around x- or y-axis : Applications of integration Volume with disc method: revolving around other axes : Applications of integration Volume with washer method: revolving around x- or y-axis : Applications of integration Volume with washer method: revolving around other axes : Applications of integration Calculator-active practice : Applications of integration. Start Course challenge. Determining concavity of intervals and finding points of inflection: algebraic : Applying derivatives to analyze functions Using the second derivative test to find extrema : Applying derivatives to analyze functions Sketching curves of functions and their derivatives : Applying derivatives to analyze functions Connecting a function, its first derivative, and its second derivative : Applying derivatives to analyze functions Solving optimization problems : Applying derivatives to analyze functions Exploring behaviors of implicit relations : Applying derivatives to analyze functions Calculator-active practice : Applying derivatives to analyze functions. Mastery unavailable.