Rhs similarity criterion

Now, let us discuss a rigorous proof of the RHS criterion. Is this possible? Of course not!

Two triangles are said to be congruent to each other if the measurements of their three sides and their three angles are exactly the same. They may be rotated or flipped. But when you carve them in a piece of paper, cut them out and place one on top of the other, they cover each other perfectly. Theorem: In two right-angled triangles, if the length of the hypotenuse and one side of one triangle, is equal to the length of the hypotenuse and corresponding side of the other triangle, then the two triangles are congruent. Theorem : In two triangles, if the three sides of one triangle are equal to the corresponding three sides SSS of the other triangle, then the two triangles are congruent.

Rhs similarity criterion

If one of the acute angles of a right triangle is congruent to an acute angle of another right triangle, then by Angle-Angle Similarity the triangles are similar. If the lengths of the corresponding legs of two right triangles are proportional, then by Side-Angle-Side Similarity the triangles are similar. If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle, then the triangles are similar. You can prove this by using the Pythagorean Theorem to show that the third pair of sides is also proportional. Taking Leg-Leg Similarity and Hypotenus-Leg Similarity together, we can say that if any two sides of a right triangle are proportional to the corresponding sides of another right triangle, then the triangles are similar. Call Now to Set Up Tutoring. Hotmath Math Homework. Download our free learning tools apps and test prep books. Right Triangle Similarity Acute Angle Similarity If one of the acute angles of a right triangle is congruent to an acute angle of another right triangle, then by Angle-Angle Similarity the triangles are similar. Leg-Leg Similarity If the lengths of the corresponding legs of two right triangles are proportional, then by Side-Angle-Side Similarity the triangles are similar. Hypotenuse-Leg Similarity If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle, then the triangles are similar.

There are, of course, three other cases to consider. No, the RHS rule is just one of several criteria to prove congruence between two right-angled triangles.

As an avid student of geometry, you likely understand the importance of congruence in shapes and figures. One of the most fundamental rules for determining congruence is the rhs congruence rule. Mastering this rule will open a deeper understanding of triangle congruence and similarity, providing a foundation for more complex geometric proofs and problem solving. In this article, you will explore the rhs congruence rule in detail. Beginning with the definition and formula, you will then see step-by-step how to apply the rule through examples and practice problems. With consistent application of the rhs congruence rule, you will strengthen your geometric reasoning and build confidence in your ability to determine congruence between triangles.

Online Math Solver ». IntMath f orum ». In geometry, two figures are said to be "congruent" if they have the same size and shape. In other words, congruent figures can be superimposed on one another. Proving that two figures are congruent is often a key step in solving geometric problems. There are several different ways to prove that two figures are congruent. In this blog post, we'll focus on one particular method known as the "RHS congruence criterion", which is written in full as Right-Hand Side congruence criterion.

Rhs similarity criterion

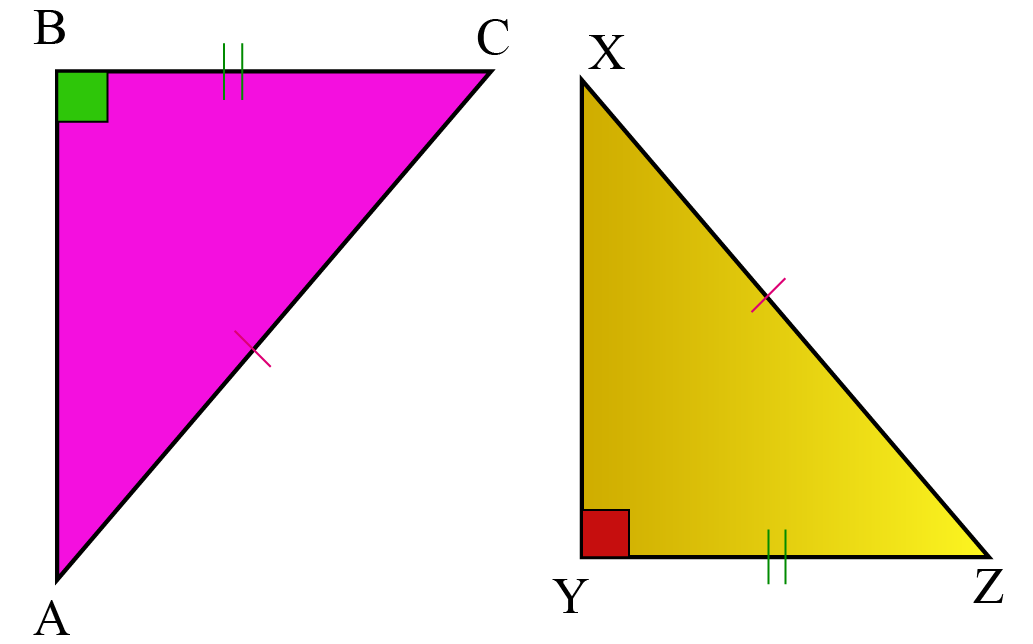
In triangles , you must have studied about congruency of triangles. However, in order to be sure that the two triangles are congruent, we do not necessarily need to have information about all sides and all angles. We use certain rules to prove the congruency of triangles. Look at the triangles given below. Can we place these triangles on each other without any gaps or overlaps? In this mini-lesson, we will explore about RHS congruency criterion by learning about its definition and proof with the help some solved examples and a few interactive questions for you to test your understanding.

Bodypainting girls

So these are going to be our similarity postulates, and I want to remind you, side-side-side, this is different than the side-side-side for congruence. So in general, in order to show similarity, you don't have to show three corresponding angles are congruent, you really just have to show two. The RHS congruence rule states that if the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the two right triangles are congruent. In these last two situations, the resulting ellipse and parallelogram no longer have the same shape as the original figures. Improved By :. Suppose that we are given a centre of enlargement O and asked to construct, using straight edge and compasses, an enlargement of some figure in the ratio a : b , where a and b are the lengths of two given intervals OF and OG on a common ray OFG. Hcf By Prime Factorization. In Triangles, if the sizes vary but the shape they have are alike, then the Triangles can be called Similar Triangles. Popular Branches MBA. Check Eligibility Free Counselling. A typical atlas will use various projections for different purposes, because each projection has its characteristic advantages and disadvantages. If you constrain this side you're saying, look, this is 3 times that side, this is 3 three times that side, and the angle between them is congruent, there's only one triangle we could make. But do you need three angles? In the language of the first section, each map is a scale drawing of Australia ignoring the curvature of the Earth , and each map is a scale drawing of the other map. The sequence of the letters tells you the order the items occur within the triangle.

Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure.

Pay close attention to the orientation of the triangles and corresponding parts. We have already noted that any two circles are similar. In this mini-lesson, we will explore about RHS congruency criterion by learning about its definition and proof with the help some solved examples and a few interactive questions for you to test your understanding. When the scale is written as a ratio of two numbers, the ratio is normally cancelled down to simplest form. Open In App. All corresponding sides are equal. The mini-lesson targeted the fascinating concept of RHS. Thirdly, since the corresponding angles are equal, each side of the image triangle is parallel to the matching side of the original triangle:. If you fix two sides of a triangle and an angle not between them, there are two nonsimilar triangles with those measurements unless the two sides are congruent or the angle is right. Actually, I want to leave this here so we can have our list. Sri Lanka. With this essential geometry skill under your belt, you'll be well on your way to tackling more complex problems. Example 1: If two triangles are congruent, prove that their respective a medians are equal b angle bisectors are equal c altitudes are equal Solution: Although these results might seem obvious, let us still go ahead and prove them rigorously.