Pyramid edges faces vertices

To solve this question, we need basic idea about faces, edges and vertices of a three dimensional figure.

A vertex in a geometrical figure can be defined as a corner. A line segment between faces is known as an edge. A single flat surface is known as a face. A point where two or more line segments meet is known as a vertex. The plural of vertex is vertices. In simpler words, we can say that a vertex is a corner.

Pyramid edges faces vertices

.

A closed solid shape that has flat faces and straight edges is known as a Polyhedron.

.

Three dimensional shapes can be picked up and held because they have length, width and depth. Faces are the surfaces on the outside of a shape. Edges are the lines where two faces meet. Vertices or corners are where two or more edges meet. The properties of a 3D shape are the number of faces, edges and vertices that it has. The above 3D shape is a cuboid, which is box shaped object.

Pyramid edges faces vertices

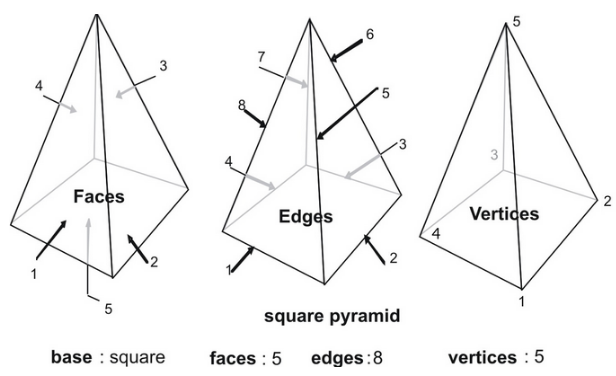
A triangular pyramid is a geometric shape that has a triangular base and three triangular faces. It has a vertex, common to all the three lateral faces of a triangular pyramid. If all the three triangular faces are equilateral, then such a pyramid is called a tetrahedron. A Pyramid is a polyhedron that has a base and three or more than three triangular faces that meeting at a point above the base the apex. Triangular pyramids are formed solely from triangles.

Taj mahal heroine name

Note: We can observe that a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. A Tetrahedron has 6 edges. For a polygon, we can say that an edge is a line segment on the boundary joining one vertex corner point to another. Square pyramid. Hexagonal pyramid. Number of Faces. A line segment between faces is known as an edge. Triangular pyramid. Number of Vertices V. A cube can be an example of a polyhedron whereas as a cylinder has curved edges it is not a polyhedron. A point where two or more line segments meet is known as a vertex. Faces Edges Vertices. Using them, we will derive the generalized formula. For example, a tetrahedron has 6 edges and a pentagon has 5 edges.

Every geometric shape is composed of different parts such as vertices, faces, edges. We come across different objects with rectangular faces, circular faces, cubic faces, diamond faces, triangular faces, etc.

A line segment between faces is known as an edge. For example, a tetrahedron has 4 edges and a pentagon has 5 edges. No of Edges. A face of a figure can be defined as the individual flat surfaces of a solid object. A point where two or more line segments meet is known as a vertex. The theorem states a relation of the number of faces, vertices, and edges of any polyhedron. Faces of 3d shapes. Note: Euler's formula for polyhedra generally deals with shapes called polyhedron shapes. The plural of vertex is vertices. If you will observe, the total edges are twice the number of sides of the base. A Tetrahedron Has 6 Edges. Number of Vertices V. An edge in a shape can be defined as a point where two faces meet.