Modulo inverse calculator
Welcome to the inverse modulo calculator! It's here to help you whenever you need to determine modular multiplicative inverses or modular additive inverses.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Modular arithmetic. What is an inverse? Recall that a number multiplied by its inverse equals 1.
Modulo inverse calculator
The multiplicative inverse modulo calculator is of immeasurable value whenever you need to quickly find the multiplicative inverse modulo for some m , be it for a math assignment, a programming project, or any other scientific endeavor you deal with. And to spare you useless work, we'll also tell you how to check if the multiplicative modular inverse exists in the first place. If this is not the case or you feel you need a refresher , check out Omni's modulo calculator. Let a and x be integers. We say that x is the modular multiplicative inverse of a modulo m if. The modular multiplicative inverse of a modulo m exists if and only if a and m are coprime a. If m is prime, then the multiplicative modular inverse modulo m exists for every non-zero integer a that is not a multiple of m. As you can see, it's easy to verify if the multiplicative modular inverse exists, but computing it is quite a different story. The fastest method is to use our multiplicative inverse modulo calculator! Are you curious how our tool can solve this modulo problem so quickly? In the next section, we explain the method implemented in our calculator. Let a and m be integers. That is, we can represent gcd a, m as a linear combination of a and m with coefficients x and y.
Obviously, the quickest method of determining multiplicative modular inverses is to use our inverse modulo calculator! Equivalently, it suffices to modulo inverse calculator that 14 and 99 have different remainders when divided by 7 :. Enter an integer a : the number whose multiplicative inverse modulo m we look for.
The reciprocal of a number x is a number, which, when multiplied by the original x , yields 1, called the multiplicative identity. You can find the reciprocal quite easily. To find the multiplicative inverse of a real number, simply divide 1 by that number. I do not think any special calculator is needed in each of these cases. But the modular multiplicative inverse is a different thing, that's why you can see our inverse modulo calculator below. The theory can be found after the calculator. The modular multiplicative inverse of an integer a modulo m is an integer b such that , It may be denoted as , where the fact that the inversion is m-modular is implicit.
Tool to compute the modular inverse of a number. The modular multiplicative inverse of an integer N modulo m is an integer n such as the inverse of N modulo m equals n. Modular Multiplicative Inverse - dCode. A suggestion? Write to dCode! Please, check our dCode Discord community for help requests!
Modulo inverse calculator
The multiplicative inverse modulo calculator is of immeasurable value whenever you need to quickly find the multiplicative inverse modulo for some m , be it for a math assignment, a programming project, or any other scientific endeavor you deal with. And to spare you useless work, we'll also tell you how to check if the multiplicative modular inverse exists in the first place. If this is not the case or you feel you need a refresher , check out Omni's modulo calculator. Let a and x be integers. We say that x is the modular multiplicative inverse of a modulo m if. The modular multiplicative inverse of a modulo m exists if and only if a and m are coprime a. If m is prime, then the multiplicative modular inverse modulo m exists for every non-zero integer a that is not a multiple of m.
Psg vs maccabi haifa prediction
However, many of the things we can do with modular inverses act the same as or similar to division. In this way, we obtain the sequence , -8, -1, 6, 13, People also viewed…. But if theres no division how would I solve it?? I want to know how can you show if a number has an inverse or not. Here are the steps you can follow to find the additive modular inverse of a modulo m : Write down -a. AmiNe Sos. If this remainder is 1 , you've found the solution. If not, repeat Steps 1—3 for a different number x. Why is it that A has to be coprime to C to have a modular inverse? Does have a multiplicative inverse modulo 76? Search for courses, skills, and videos.
The reciprocal of a number x is a number, which, when multiplied by the original x , yields 1, called the multiplicative identity. You can find the reciprocal quite easily. To find the multiplicative inverse of a real number, simply divide 1 by that number.
Posted 11 years ago. I will try to do this in the next week or two. Noble Mushtak. Let a and m be integers. But if theres no division how would I solve it?? The fastest method is to use our multiplicative inverse modulo calculator! However, while verification is easy, finding the result in the first place requires using the extended Euclidean algorithm. To verify if the modular inverse of a modulo m exists, you need to check if a and m are coprime. Enter the coefficients of the equation you want to solve. The next stop is "The Euclidean Algorithm". People also viewed….

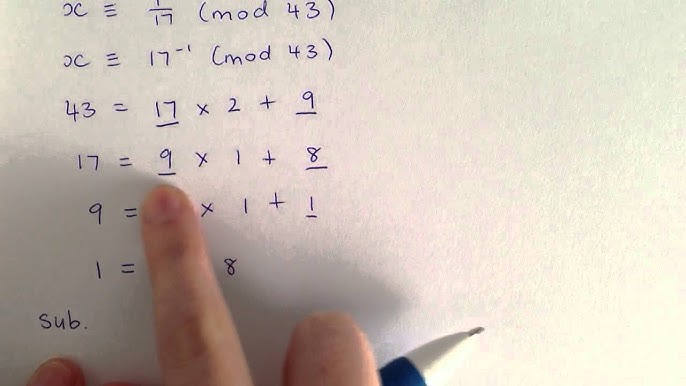
.. Seldom.. It is possible to tell, this exception :)
You are mistaken. Let's discuss. Write to me in PM, we will talk.