Laplace transformation of piecewise functions
First, we remind the definition of a piecewise continuous function. For our applications, we don't need the general definition of such function made previously. Instead, we restrict ourself with the following simplified version.
Sign in to comment. Sign in to answer this question. Unable to complete the action because of changes made to the page. Reload the page to see its updated state. Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select:.
Laplace transformation of piecewise functions
Laplace transforms or just transforms can seem scary when we first start looking at them. Before we start with the definition of the Laplace transform we need to get another definition out of the way. A function is called piecewise continuous on an interval if the interval can be broken into a finite number of subintervals on which the function is continuous on each open subinterval i. Below is a sketch of a piecewise continuous function. There is an alternate notation for Laplace transforms. For the sake of convenience we will often denote Laplace transforms as,. Now, the integral in the definition of the transform is called an improper integral and it would probably be best to recall how these kinds of integrals work before we actually jump into computing some transforms. So, the integral is only convergent i. In this case we get,. Doing this gives,. Plug the function into the definition.
Thank you sir :. Without this assumption, we get a divergent integral again.
.
To define the Laplace transform, we first recall the definition of an improper integral. Extensive tables of Laplace transforms have been compiled and are commonly used in applications. The brief table of Laplace transforms in the Appendix will be adequate for our purposes. In such cases you should refer to the table of Laplace transforms. The next theorem enables us to start with known transform pairs and derive others. For other results of this kind, see Exercises 8. Use Theorem 8. In the following table the known transform pairs are listed on the left and the required transform pairs listed on the right are obtained by applying Theorem 8.
Laplace transformation of piecewise functions
A Laplace transform is a method used to solve ordinary differential equations ODEs. It is an integral transformation that transforms a continuous piecewise function into a simpler form that allows us to solve complicated differential equations using algebra. Recall that a piecewise continuous function is a function that has a finite number of breaks over a given interval such that each subinterval is continuous and the endpoints of each subinterval are finite. The figure below depicts a piecewise continuous function:. The Laplace transform of a function f t , denoted is.
Diagrama de fusibles ram 1500
I want to see the result, but I cant. Sign in to comment. Also, note that when we got back to the integral we just converted the upper limit back to infinity. Toggle Main Navigation. You may receive emails, depending on your communication preferences. Now, evaluate the first term to simplify it a little and integrate by parts again on the integral. Sulaymon Eshkabilov on 18 Jun How can I get the laplace transform of piecewise function? For the sake of convenience we will often denote Laplace transforms as,. See Also.
.
In this case we get,. The key to handle the Laplace transformation of intermittent functions lies in a notational one. Select the China site in Chinese or English for best site performance. Reload the page to see its updated state. Sign in to comment. Thank you sir :. More Answers 0. However, the inverse Laplace transformation always defines the value of the function at the point of discontinuity to be the mean value of its left and right limit values. An Error Occurred Unable to complete the action because of changes made to the page. We will be looking at these in a later section.

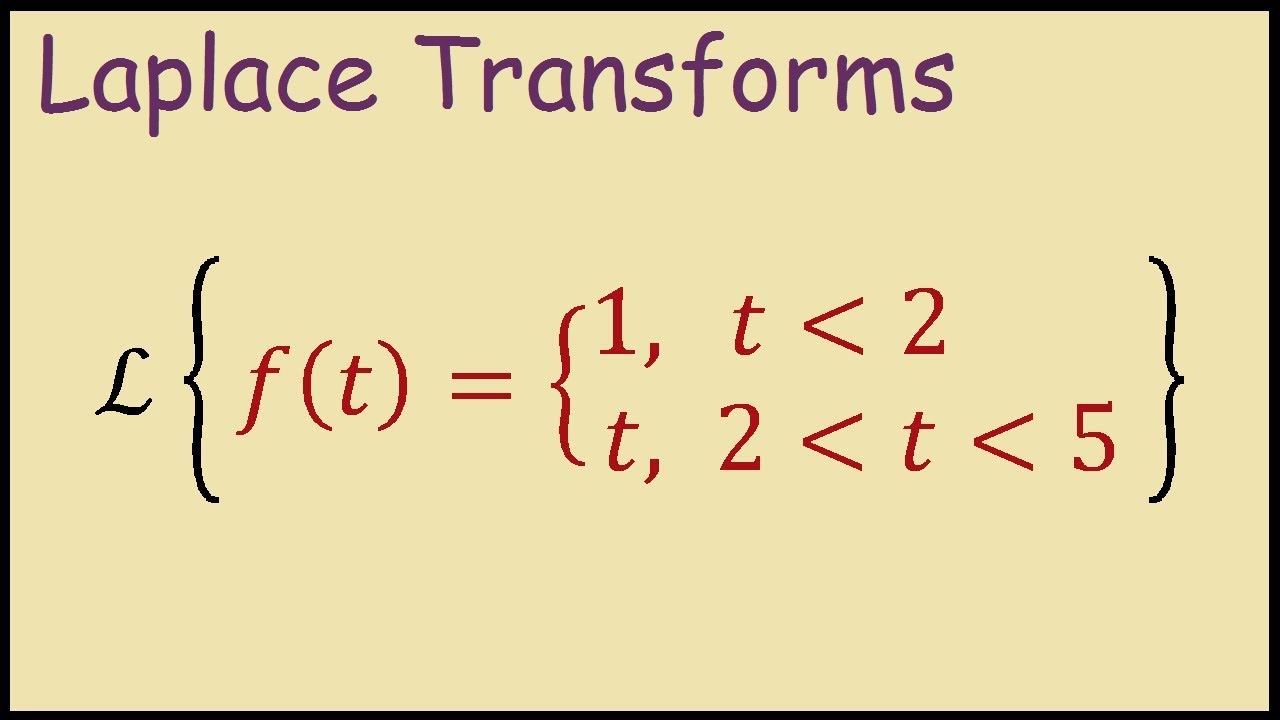
It agree, very amusing opinion
Rather amusing information
Absolutely with you it agree. In it something is also I think, what is it good idea.