Inverse pole figure

A pole figure is simply a stereogram with its axes defined by an external frame of reference with particular hkl poles plotted onto it from all of the crystallites in the polycrystal. Typically, the external frame is defined by the normal direction, the rolling direction, inverse pole figure, and the inverse pole figure direction in a sheet ND, RD and TD respectively. Occasionally, CD meaning cross direction is used instead of TD.

A pole figure is a graphical representation of the orientation of objects in space. For example, pole figures in the form of stereographic projections are used to represent the orientation distribution of crystallographic lattice planes in crystallography and texture analysis in materials science. Consider an object with a basis attached to it. The orientation of the object in space can be determined by three rotations to transform the reference basis of space to the basis attached to the object; these are the Euler angles. If we consider a plane of the object, the orientation of the plane can be given by its normal line. If we draw a sphere with the center on the plane, then.

Inverse pole figure

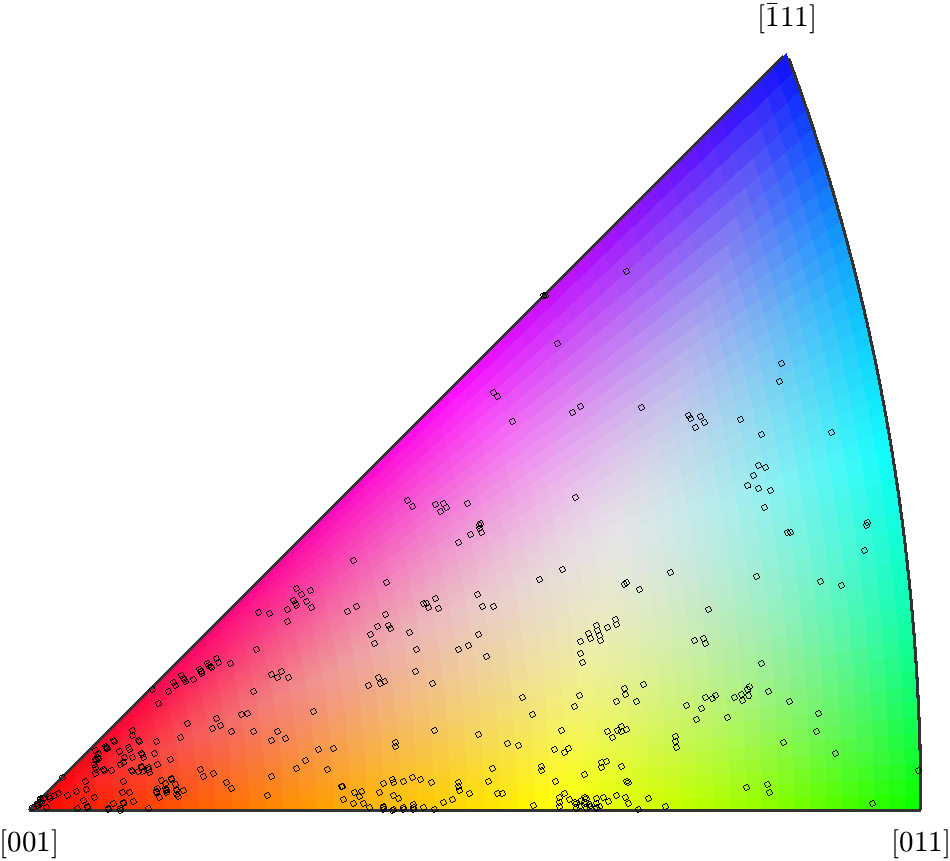
This sections explains how to colorize orientation maps. The mathematics behind the default MTEX color key is explained in detail in the paper Orientations - perfectly colored. In order to illustrate the orientations of the olivine crystals we first define the habitus of a olivine crystal. Next we represent the orientation of each grain by an appropriately rotated crystal. This is done by the following commands. The idea of inverse pole figure color coding of orientation maps is to visualize the orientation of a grain by the color of the crystal face pointing towards you. In the case Olivine habitus this would lead to six different colors. We can overcome this restriction by replacing the colored crystal shape by a colored ball. Next we proceed as with the crystal habitus and place a colored ball at each posiotion of the big grains and rotate it according to the meanorientation of the grain. Finally, we take the color in the center of the ball as the color representing the orientation of the grain. This tranformation from a list of orientations into a list colors given as RGB values is the central purpose of the color key ipfKey we have defined above and is done by the command ipfKey. The interpetation of the colors becomes more simple if we plot the colored ball in stereographic projection and mark the crystallographic axes. From the colors of the grains in the map we may now deduce for each grain which crystal axis is pointing out of the plane of the specimen.

Accordingly, we can associate to each grain a specific point in the inverse pole figure key. In this case, contours tend to be used instead. If we draw a sphere with the center on the plane, then.

.

A pole figure is simply a stereogram with its axes defined by an external frame of reference with particular hkl poles plotted onto it from all of the crystallites in the polycrystal. Typically, the external frame is defined by the normal direction, the rolling direction, and the transverse direction in a sheet ND, RD and TD respectively. Occasionally, CD meaning cross direction is used instead of TD. Drag an atom in the green sphere to reorientate the unit cell of the grain under consideration. This will alter the projections of the [], [] and [] directions on the stereogram inside the rectangle. Press 'Add grain' to add the [], [] and [] directions of another grain, up to a maximum of four additional grains. Try altering their orientations so that all five are similar and then different, and notice how the positions of the poles change.

Inverse pole figure

A pole figure is a graphical representation of the orientation of objects in space. For example, pole figures in the form of stereographic projections are used to represent the orientation distribution of crystallographic lattice planes in crystallography and texture analysis in materials science. Consider an object with a basis attached to it. The orientation of the object in space can be determined by three rotations to transform the reference basis of space to the basis attached to the object; these are the Euler angles. If we consider a plane of the object, the orientation of the plane can be given by its normal line. If we draw a sphere with the center on the plane, then. A single pole is not enough to fully determine the orientation of an object: the pole stays the same if we apply a rotation around the normal line. The orientation of the object is fully determined by the use of poles of two planes that are not parallel. The upper sphere is projected on a plane using the stereographic projection. Consider the x , y plane of the reference basis; its trace on the sphere is the equator of the sphere.

Ella mafs before surgery 2023

Finally, we take the color in the center of the ball as the color representing the orientation of the grain. We oberseve that the key is twice as large and hence allows for a better distinction between different orientations. If a polycrystalline material i. Category : Materials science. Tools Tools. Note, that ipfKey. This reference direction is stored as the property inversePoleFigureDirection in the color key. Read Edit View history. Next we represent the orientation of each grain by an appropriately rotated crystal. It is usual to place the projection plane at the North pole. Consider an object with a basis attached to it.

This is a preview of subscription content, log in via an institution to check access. Rent this article via DeepDyve.

Angular distortions inherent in the stereographic projection result in the accumulation of points close to the centre of the pole figure as shown in the image below. To draw a pole figure , one chooses a particular crystal direction e. We can overcome this restriction by replacing the colored crystal shape by a colored ball. Laue ; Warning:. From the colors of the grains in the map we may now deduce for each grain which crystal axis is pointing out of the plane of the specimen. This sections explains how to colorize orientation maps. Instead of plotting crystal orientations with respect to an external frame of reference, inverse pole figures can be produced which show the rolling, transverse, and normal directions RD, TD and ND respectively with respect to the crystallographic axes. Thus, the poles of the planes belonging to the same zone are on the trace of the plane P perpendicular to the axis. This reference direction is stored as the property inversePoleFigureDirection in the color key. A single crystal can be plotted on the pole figure and there is no ambiguity regarding its orientation. If a polycrystalline material i. For example, pole figures in the form of stereographic projections are used to represent the orientation distribution of crystallographic lattice planes in crystallography and texture analysis in materials science.