How to find oblique asymptotes using limits
We have shown how to use the first and second derivatives of a function to describe the shape of a graph. In this section, we define limits at infinity and show how these pinterest emoji affect the graph of a function. We begin by examining what it means for a function to have a finite limit at infinity, how to find oblique asymptotes using limits. Then we study the idea of a function with an infinite limit at infinity.
We use MathJax. Many functions exhibit asymptotic behavior. Graphically, that is to say that their graph approaches some other geometric object usually a line as the graph of the function heads away from the area around the origin. In other words, asymptotic behavior involves limits, since limits are how we mathematically describe situations where a function approaches a value. In college algebra, you may have learned how to locate several type of asymptotes.
How to find oblique asymptotes using limits
.
Formal Definitions Earlier, we used the terms arbitrarily close, arbitrarily large, and sufficiently large to define limits at infinity informally.
.
An oblique or slant asymptote is a dashed line on a graph, describing the end behavior of a function approaching a diagonal line where the slope is neither zero nor undefined. A function may have a horizontal or an oblique asymptote; it cannot have both. Like horizontal asymptotes, oblique asymptotes can cross the function. They can be negative and extend to infinity. Also, a function may have a maximum of two oblique asymptotes but can have infinitely many vertical asymptotes. Thus, we get the equation of line l , which is the oblique asymptote of f x. However, there are a few more direct methods to find the oblique asymptotes of various functions, which we will discuss below. So, we must use long division to find the quotient.
How to find oblique asymptotes using limits
We use MathJax. Many functions exhibit asymptotic behavior. Graphically, that is to say that their graph approaches some other geometric object usually a line as the graph of the function heads away from the area around the origin. In other words, asymptotic behavior involves limits, since limits are how we mathematically describe situations where a function approaches a value.
Major league baseball divisional standings
Graphically, that is to say that their graph approaches some other geometric object usually a line as the graph of the function heads away from the area around the origin. We have shown how to use the first and second derivatives of a function to describe the shape of a graph. Since the other terms will not head toward zero, we identify those other terms as part of the asymptote. We use MathJax. To find possible locations for the vertical asymptotes, we check out the domain of the function. In college algebra, you may have learned how to locate several type of asymptotes. We now turn our attention to a more precise definition for an infinite limit at infinity. Earlier, we used the terms arbitrarily close, arbitrarily large, and sufficiently large to define limits at infinity informally. An oblique linear asymptote occurs when the graph of a function approaches a line that is neither horizontal nor vertical. First, using long division of polynomials, we can write. We say a function has a negative infinite limit at infinity and write. Although these terms provide accurate descriptions of limits at infinity, they are not precise mathematically. Step 2: Find the intercepts. We can extend this idea to limits at infinity.
In my experience, students often hit a roadblock when they see the word asymptote. What is an asymptote anyway?
We now look at the definition of a function having a limit at infinity. The algebraic limit laws and squeeze theorem we introduced in Introduction to Limits also apply to limits at infinity. In this case, the function may have some oscillatory behavior. We illustrate how to use these laws to compute several limits at infinity. Step 6. Only if the first one-sided limit is not infinite does it become necessary to check the other one-sided limit. Solution a. Recognize an oblique asymptote on the graph of a function. The end behavior for rational functions and functions involving radicals is a little more complicated than for polynomials. Step 4: To check for vertical asymptotes, look at where the denominator is zero. Once you have confirmed a vertical asymptote, it is not necessary to check the other one-sided limit at that same point. Since asymptotes are lines, they are described by equations, not just by numbers. Determine the point on the graph where a cusp is located. Consider a rational function.

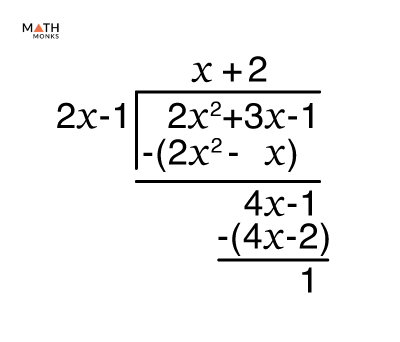
YES, this intelligible message
Also that we would do without your brilliant idea