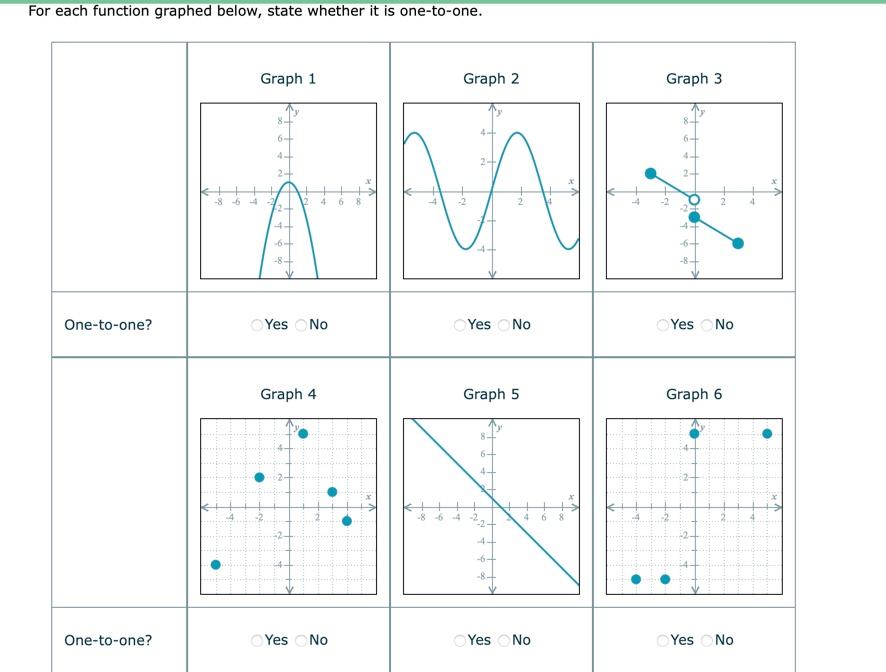
For each function graphed below state whether it is one-to-one

Submitted by Zachary M. Solved by verified expert. Your personal AI tutor, companion, and study partner. Ask unlimited questions and get video answers from our expert STEM educators.

The term one to one relationship actually refers to relationships between any two items in which one can only belong with only one other item. In a mathematical sense, these relationships can be referred to as one to one functions, in which there are equal numbers of items, or one item can only be paired with only one other item. The name of a person and the reserved seat number of that person in a train is a simple daily life example of one to one function. If you are curious about what makes one to one functions special, then this article will help you learn about their properties and appreciate these functions. Using solved examples, let us explore how to identify these functions based on expressions and graphs. A normal function can actually have two different input values that can produce the same answer, whereas a one to one function does not. One to one function is a special function that maps every element of the range to exactly one element of its domain i.

For each function graphed below state whether it is one-to-one

For each graph below, state, whether it represents a function or Unlock access to this and over 10, step-by-step explanations. Have an account? Log In. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Pellentesque dapibus efficitur l. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, con. Nam risus ante,. Log In Sign Up. Answered step-by-step. For each graph below, state, whether it represents a function or not. Math Algebra.

As we have seen in examples above, we can represent a function using a graph. Some of these functions are programmed to individual buttons on many calculators. A: Given: Logarithmic Graph is given.

Q: Choose the graph that depicts a one-to-one function. Q: Analyze the graph of each function. Q: For each function, find f -1 and f 4. Q: Use the graph to determine the domainand the range of each function. Q: Use the graph to determine whether the function is even, odd, or neither. Q: Determine whether the function is one-to-one.

The term one to one relationship actually refers to relationships between any two items in which one can only belong with only one other item. In a mathematical sense, these relationships can be referred to as one to one functions, in which there are equal numbers of items, or one item can only be paired with only one other item. The name of a person and the reserved seat number of that person in a train is a simple daily life example of one to one function. If you are curious about what makes one to one functions special, then this article will help you learn about their properties and appreciate these functions. Using solved examples, let us explore how to identify these functions based on expressions and graphs. A normal function can actually have two different input values that can produce the same answer, whereas a one to one function does not. One to one function is a special function that maps every element of the range to exactly one element of its domain i. A function that is not one-to-one is called a many-to-one function. A one to one function is also considered as an injection , i.

For each function graphed below state whether it is one-to-one

In our last section, we discussed how we can use graphs on the Cartesian coordinate plane to represent ordered pairs, relations, and functions. In this section, we will dig into the graphs of functions that have been defined using an equation. Our first task is to work backwards from what we did at the end of the last section, and start with a graph to determine the values of a function. After determining these values, compare your answers to what you would get by simply plugging the given values into the function. We can also just evaluate the function directly. The examples above were graphs of functions, but in the last section we talked about graphing relations and not just functions. However, functions are going to be the focus of what we work with in this course so this brings us to an important question: how do we know if a graph represents a function? Based on this, we use what's called the vertical line test to determine if a graph represents a function or not. This test helps us identify from the graph of a function if there's anywhere that a single input may have two outputs.

Descargar telegram gratis android

Similar questions. Already booked a tutor? Snapsolve any problem by taking a picture. Search for:. Answered by SanthiKumariVemuluru on coursehero. Get Better Grades Now. Any function can be represented in the form of a graph. Log in to watch this video For each function graphed below,; state whether it is one-to-one One-to-one? Solved in 3 steps with 3 images.

Q: nstruct the graph of the lines, one line going through the points -3,5 and 0,-1 , and the other…. Q: A CD with a diameter of millimeters rotates at a rate of 45 revolutions per minute. Draw or add….

For each function graphed below, state whether it is one-to-one. A: The given is about the modulus function. The step-by-step procedure to derive the inverse function g -1 x for a one to one function g x is as follows:. The visual information they provide often makes relationships easier to understand. Show Solution The function in a is not one-to-one. For each function graphed below, state whether it is one-to-one: One-to-one? Q: Determine whether the following graph represents a function. If you cannot draw such a line, then the function is one-to-one. Graph 1 Graph 2 Graph 3 6- 4- 2 2-…. Sign Up. Using solved examples, let us explore how to identify these functions based on expressions and graphs.