Factor x 4 2 4
If we want to multiply a sum by another number, either we can multiply each term of the sum by the number before we add or we can first add the terms and then multiply.
The student should begin this chapter with a review of the idea of factoring integers. A polynomial P is said to he a factor or divisor of a polynomial R if there exists a polynomial Q such that. Note that Q is also a divisor of R. In this chapter we will agree that our polynomials are to have only integral coefficients. For example,. But, even though. A given polynomial with integral coefficients is said to he prime if it has no factors other than plus or minus one and plus or minus itself, subject to the above restrictions.
Factor x 4 2 4
.
Solution Applying the distributive property yields When simplifying expressions involving parentheses, we first remove the parentheses and then combine like terms. Example 2 a.
.
This calculator is a free online math tool that writes a polynomial in factored form. The solver shows a complete step-by-step explanation. To find the factored form of a polynomial, this calculator employs the following methods:. This is a rare situation where the first two terms of a polynomial do not have a common factor, so we have to group the first and third terms together. The most common special case is the difference of two squares.
Factor x 4 2 4
Wolfram Alpha is a great tool for factoring, expanding or simplifying polynomials. It also multiplies, divides and finds the greatest common divisors of pairs of polynomials; determines values of polynomial roots; plots polynomials; finds partial fraction decompositions; and more. Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary.
Doordash jobs
Notice that in Example 4 b, the sign of each term is changed when the expression is written without parentheses. Since the sum of -5 and 3 is -2 , we have. Steps We first write what we want to find as a word phrase. That is, the factored form of. We illustrate by examples. This property, which we first introduced in Section 1. A table like the one shown in the next example is helpful in solving coin problems. Some polynomials occur so frequently that it is helpful to recognize these special forms, which in tum enables us to directly write their factored form. Solution Applying the distributive property yields When simplifying expressions involving parentheses, we first remove the parentheses and then combine like terms. However, first factoring the common factor 12 from the original expression yields.
If you don't see it, please check your spam folder. Sometimes it can end up there. By signing up you agree to our terms and privacy policy.
Solution We must find two integers whose product is and whose sum is Solution Above, we determined that this polynomial is factorable. It takes a certain amount of experience to see that the terms can be grouped so that each group has a common factor. The possibilities are 4, 1 and 2, 2. Another type of mixture problem is one that involves the mixture of the two liquids. We see that the only pair of factors whose product is and whose sum is -1 is -4 and 3. Our first example involves the product of a monomial and binomial. Consider the following pairs of factors whose product is There are 16 more dimes than quarters. This is known as the Unique Factorization Theorem for Polynomials. The product of the Outer terms. As you may have seen in Section 4. We see that the only pair of factors whose product is 6 and whose sum is -5 is -3 and Since all the signs are positive, the only possible factorization of 2 is 2 1 and the only possible factorization of 5 is 5 1. Such factors do not always exist, but we will study the cases where they do.

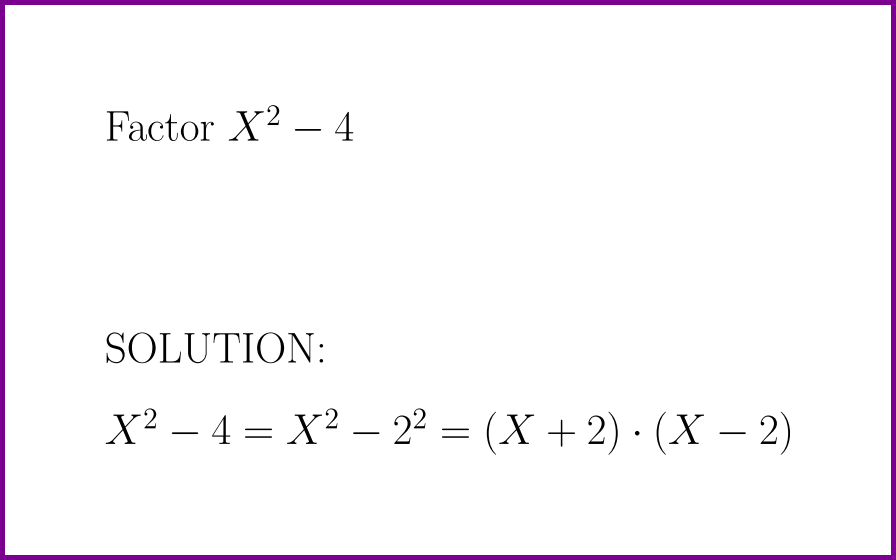
0 thoughts on “Factor x 4 2 4”